What is the partial dependency of your decision on a specific data point?
The financial industry has made a big step towards adopting the implementation of advanced machine learning models in their credit decisioning. However, the implementation of real time scoring methods supported by machine learning is still a paradox. Institutional heads become worried implementing black box models without understanding the transformational process the data goes through. Risk managers would like to understand computations that take place before a decision is arrived at. In most cases, this is a complex task. Take an example of a random forest model which generates a decision from a forest or optimal selection of many decision trees and predicts whether someone will default or not. In most cases, business would like to generate rules from intelligent processes which will guide the business in deciding what an ideal client profile will look like.
In digital lending, the profile attributes generated will eventually be introduced into the scoring process with points accorded to each feature. Unfortunately, in machine learning, a combination of attributes affects the overall performance of the model and selecting limited features, especially where you have hundreds of important features will lessen the quality of your model. That is why the accuracy of most models implemented in credit reference bureau in Kenya on the digital lending frontier hardly meet the client’s expectations. Lenders eventually must invest in a debt collection team to follow up unpaid debts. In fact, CRB agencies achieve a 10-30% default rate, assuming all clients have to repay their loans by the due date. The easiest way at the initial stages of introducing machine learning into ordinary business processes in an organization is to attempt to explain how different (most important variables) affect the main response variable thanks to Friedman (2001) who introduced the partial dependency plots.
A partial dependence plot may be viewed as a pictorial representation of linear regression model coefficients. While most people use traditional regression models which allow us to decipher considerable knowledge by breaking down the structure and interpretation of the model in examining its coefficients. Often, we find ourselves running more advanced and complex models which require lots of tuning, stress testing and optimization. These models are such as the XGBoost family, Random Forest Models, support vector machines, etc. In such cases, you hardly find methods of estimating dependency of the response variable on the predictor variables. It becomes difficult to interpret some of these models. Occasionally, we find ourselves trying to convince the executives by using model evaluation metrics such as precision, recall, accuracy, ROC AUC etc. in a bid to explain how far we can fly with the new rocket (ML Model). To tell a more interesting story and connect with the business, consider making use of partial dependency plots.
Friedman (2001) encountered a similar case and probably as a data scientist, it became challenging for him to interpret the data. To address this difficulty for his gradient boosting machine, Friedman proposed the use of partial dependence plots. Partial dependency plots will help you explain how each dependent variable in your dataset influences the response. It gets very interesting if you as a data analyst can explain things from this perspective.
Digital Lending Case of Dependency Plotting
Let us assume we want to predict the likelihood of a customer repaying his digital loan as an output variable (represented as True/False where True stands for – likelihood of repaying in time & False -likelihood of not repaying in time) and two predictor variables Age & income change monthly. Please remember the data used herein is randomly generated for purposes of sharing knowledge. The key question here will be, what is the effect of the salary change on the ability to repay his loan on time. The following table represents data of actual happenings. We will train a machine learning model which will learn the different combinations that will determine repay ability.
|
Age |
Income change |
Actual Case |
I decided to run two high performance models, namely Random Forest & XGoost. Using an AUC ROC measure, my models had an accuracy of 70%. In a real-world assignment, this isn’t good at all but with only two predictors, I would say that is a good start. Apparently, income change month on month seems to be a stronger predictor as compared to age.
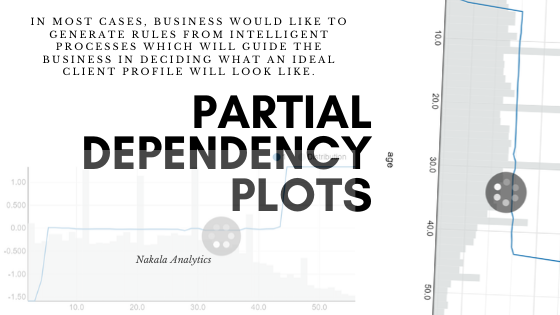
Back to the main analysis, the partial plot. Plotting a partial dependency plot shows some interesting information. As you may know a partial dependence plot shows the dependence of the predicted response to a single feature. The x axis displays the value of the selected feature, while the y axis displays the partial dependence. The value of the partial dependence is by how much the log-odds are higher or lower than those of the average probability. The log-odds for a probability p are defined as log (p / (1 - p)). They are strictly increasing, i.e. higher log odds mean higher probability. The below plot simply tells me that the correlation between ability to repay in time and age becomes more significant starting at age 45.

What does that mean? This simply tells us that people of age 45 and above are less risky.
Applying the same method on other variables creates a client profile that can be used to define the qualifies of a good customer for your business. Share your feedback.